[머신러닝] Linear Regression - 지구 온도 변화 분석

 

 

 

2022.07.05 - [Studying/Machine Learning] - [머신러닝] Linear regression(선형 회귀) 구현

 

[머신러닝] Linear regression(선형 회귀) 구현

저번 포스팅에 이어서 실제 데이터로 지구 온도 변화를 분석해 보려고 한다.

 

우선 영상을 확인해보자

https://www.youtube.com/watch?v=3sqdyEpklFU

 

기온이 점점 상승하고 있다는 것을 알 수 있고 이를 선형 회귀로 분석해보겠다.

 

여기서 지표는 Global temperature anomaly라는 지표를 사용할건데

 

이 값은 어떤 기준 온도를 설정해놓고 그것과의 차이를 나타낸 것이다.

양수라면 평소보다 따뜻한 기온이고, 음수라면 평소보다 차가운 기온이다.

 

---

그러면 NOAA(National Oceanic and Atmospheric Administration) 홈페이지에서 데이터를 가져오겠다.

 

홈페이지에 들어가서 csv파일을 받아도 되지만 urllib라는 모듈을 통해 가져오겠다.

 

from urllib.request import urlretrieve

URL = "https://www.ncei.noaa.gov/cag/time-series/global/globe/land/ann/12/1880-2021.csv"
#파일의 URL
urlretrieve(URL, 'temperature.csv')
#저장할 파일명

파일을 받았고 이 데이터를 numpy 패키지를 이용해 불러오겠다.

import numpy

fname = '/content/temperature.csv' #파일의 경로

year, temp_anomaly = numpy.loadtxt(fname, delimiter=',', skiprows=5, unpack=True)

 

먼저 이 데이터를 pyplot으로 시각화해보겠다.

from matplotlib import pyplot
%matplotlib inline

pyplot.plot(year, temp_anomaly);

x축이 연도고 y축이 anomaly data다.

 

---

여기까지 data를 가져왔고 이제 linear regression을 위해 직선을 정의하겠다.

$$f(x_i) = wx + b$$

다음은 cost function을 정의하겠다.

 

$$\frac{1}{n} \sum_{i=1}^n (y_i - f(x_i))^2 = \frac{1}{n} \sum_{i=1}^n (y_i - (wx_i + b))^2$$

 

 

이제 cost function을 구하고자 하는 변수로 미분한 뒤 0이 되도록 하는 값을 찾으면 된다.

 

 

먼저 b에 대해 미분을 하고

$$\frac{\partial{J(w,b)}}{\partial{b}} = \frac{1}{n}\sum_{i=1}^n -2(y_i - (wx_i+b)) = \frac{2}{n}\left(b + w\sum_{i=1}^n x_i -\sum_{i=1}^n y_i\right) = 0$$

 

위 식을 만족하는 b에 대해서 정리하면 

 

$$b = \bar{y} - w\bar{x}$$

 

 

여기서 bar x와 bar y는 다음과 같다.

$$\bar{x} = \frac{\sum_{i=1}^n x_i}{n}$ , $\bar{y} = \frac{\sum_{i=1}^n y_i}{n}$$

 

이제 w에 대해서 미분을 하면

$$\frac{\partial{J(w,b)}}{\partial{w}} = \frac{1}{n}\sum_{i=1}^n -2(y_i - (wx_i+b))x_i = \frac{2}{n}\left(b\sum_{i=1}^nx_i + w\sum_{i=1}^n x_i^2 - \sum_{i=1}^n x_iy_i\right)$$

여기에 아까의 b를 대입한 후 0이 되는 w값을 구하면 다음과 같다.

$$w = \frac{\sum_{i=1}^ny_i(x_i-\bar{x_i})}{\sum_{i=1}^nx_i(x_i-\bar{x_i})}$$

 

 

이렇게 계산을 통해 w와 b값을 구했다.

 

---

이제 코드를 통해서 적용해 보겠다.

 

w = numpy.sum(temp_anomaly*(year - year.mean())) / numpy.sum(year*(year - year.mean())) 
b = a_0 = temp_anomaly.mean() - w*year.mean()

print(w)	# 0.01164682485629444
print(b)	# -22.619526248399488

아까의 그래프에 선을 그어서 확인해보겠다.

 

pyplot.figure(figsize=(10, 5))

pyplot.plot(year, temp_anomaly) 
pyplot.plot(year, reg, 'k--', linewidth=2, label='Linear regression')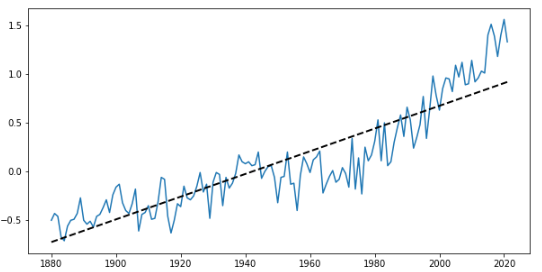

데이터와 유사한 직선이 그려진 것을 확인할 수 있다.