이전의 두 포스트에서는 데이터와 잘 맞는 직선을 찾는 linear regression을 했는데
예측 값이 떨어져 있다면 이 모델로는 예측이 어려울 것이다.
가장 대표적인 것이 binary classification인데 예측값이 0 또는 1이다.
이때 이 예측값을 확률로 표현한 다음 특정 값 이상이면 1 아니면 0으로 분류한다.
이러한 문제에 적용하는 방법이 Logistic Regression이다.
이론
logistic regression을 진행하기 위해서는 출력 값을 0과 1로 맞춰주어야 한다.
이를 위해 다음과 같은 logistic function을 사용한다.
$$\sigma(z) = \frac{1}{1 + e^{-z}}$$
입력 데이터를 x, 실제 class 값을 y, 예측된 출력 값을 y_hat이라 하면 x는 다음의 두 가지 변환을 거쳐 y_hat이 된다.
$$z = wx + b$$
$$\hat{y} = \sigma(z)$$
여기서 목표는 y와 y_hat을 가깝게 하는 w와 b를 찾는 것이다.
Logistic Function
logistic function을 그래프로 보면 다음과 같다.
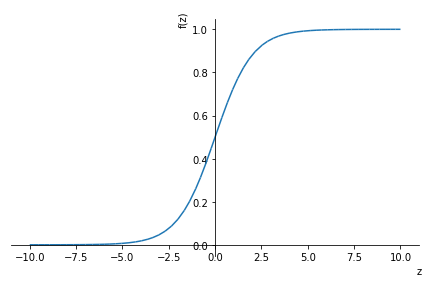
z=0일 때 출력 값이 0.5이고, 양수일 때 1, 음수일 때 0으로 가까워지게 된다.
이렇게 z값을 0과 1 사이로 표현할 수 있게 되었다.
Data Making
이제 직접 데이터를 만들어서 진행해 보겠다.
x_data = numpy.linspace(-5, 5, 100)
w = 2
b = 1
#y = 2*x_data+1
numpy.random.seed(0) #시드를 고정하여 매번 같은 결과를 내도록
z_data = w * x_data + b + numpy.random.normal(size=len(x_data))#데이터에 noise 추가
y_data = 1 / (1+ numpy.exp(-z_data))
pyplot.scatter(x_data, y_data, alpha=0.4);
이제 실제 class 값을 정해주기 위해 where함수로 0.5보다 큰 값을 1, 작은 값을 0으로 변환하겠다.
y_data = numpy.where(y_data >= 0.5, 1, 0)
pyplot.scatter(x_data, y_data, alpha=0.4);
Cost Function
이제 y_hat과 실제 y가 가깝게 되도록 하는 w와 b를 찾으려면 cost function을 정의해야 한다.
전의 linear regression에는 MSE를 사용했지만 해당 함수는 convex(볼록함)한 형태기 때문에
$$\frac{1}{n} \sum_{i=1}^n (y_i - (wx_i + b))^2$$
아래와 같이 sigmoid function을 사용해서 convex하지 않게 만들어 준다.
$$\frac{1}{n} \sum_{i=1}^n (y_i - \sigma(wx_i + b))^2$$

하지만 이 함수의 최솟값을 gradient descent를 이용해 구하면 기울기가 0인 지점에서 멈추고
local minimum에 도달하게 된다.
그럼 cost function을 다시 생각해보아야 한다.
y=1인 경우 예측값이 1에 가깝길 바라지만 0에 가깝게 나왔다면 cost function의 값이 매우 커야 한다.
이를 만족시킬 수 있는 함수는 log를 이용해 만들 수 있다.
$$L = \begin{cases} -log(\sigma(wx+b)),\;if\;y=1\\ -log(1-\sigma(wx+b)),\;if\;y=0 \end{cases}$$
y값이 0 또는 1이기 때문에 다음과 같이 정리할 수 있다.
$$L = -y \log(\sigma(wx+b)) - (1-y)\log(1-\sigma(wx+b))$$
이 식이 logistic function에서 cost function이 된다.
Code
이제 이 전체 프로세스를 코드로 구현해보겠다.
우선 cost function을 정의하겠다.
w, b, x, y = sympy.symbols('w b x y')
logistic = 1/(1+ sympy.exp(-w*x-b)) # x를 0에서 1사이로 표현
Loss = -y*sympy.log(logistic) - (1-y)*sympy.log(1-logistic) # cost function
x변환, logistic 모델, cost function을 정의해보겠다.
from autograd import numpy
from autograd import grad
def logistic(z):
return 1 / (1 + numpy.exp(-z))
def logistic_model(params, x):
w = params[0]
b = params[1]
z = w * x + b
y = logistic(z)
return y
def log_loss(params, model, x, y):
y_pred = model(params, x)
return -numpy.mean(y * numpy.log(y_pred) + (1-y) * numpy.log(1 - y_pred))
기울기 계산을 위해서는 autograd를 통해서 gradient값을 구해보겠다.
numpy.random.seed(0)
params = numpy.random.rand(2) #parameter 초기화
gradient = grad(log_loss) # logistic loss 기울기를 계산하는 함수 정의
gradient(params, logistic_model, x_data, y_data) # 기울기 계산
# array([-0.42734877, 0.08274066])
w와 b에 대해 기울기를 구한다.
새로운 조건을 추가해서 5000번의 반복 수 외에 기울기 값이 0.001보다 작아지면 멈추도록 설정하겠다.
max_iter = 5000
i = 0
descent = numpy.ones(len(params))
while numpy.linalg.norm(descent) > 0.001 and i < max_iter:
descent = gradient(params, logistic_model, x_data, y_data)
params = params - descent * 0.01
i += 1
print('Optimized value of w is {} vs. true value: 2'.format(params[0]))
print('Optimized value of b is {} vs. true value: 1'.format(params[1]))
#evaluation metrics used in real world dataset
print('Exited after {} iterations'.format(i))
예측된 값을 plot 해보면 다음과 같다.
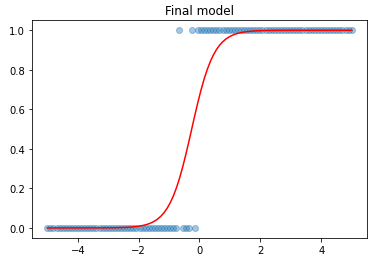
여기서 기준값을 0.5로 정하고 이것보다 크면 1, 작으면 0으로 분류를 하는 함수를 만들겠다.
def decision_boundary(y):
return 1 if y >= .5 else 0
모든 점을 함수에 넣어서 판단해야 하는데 오래 걸리기 때문에 numpy의 vectorize함수를 사용하겠다.
decision_boundary = numpy.vectorize(decision_boundary)
그래프로 데이터를 확인해보겠다.
def classify(predictions):
return decision_boundary(predictions)
final_predictions = classify(logistic_model(params, x_data))
pyplot.scatter(x_data, y_data, alpha=0.4,
label='true value')
pyplot.scatter(x_data, final_predictions, alpha=0.4,
label='prediciton')
pyplot.title('Score: [{}] / [{}]'.format(sum(final_predictions == y_data), len(y_data)))
pyplot.legend()
pyplot.show()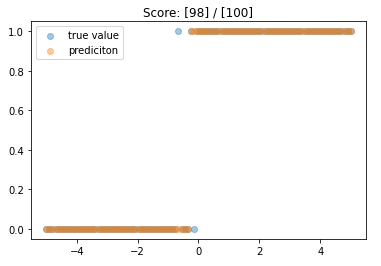
98퍼센트의 정확도로 예측을 했다.
다음 포스트에서는 실제의 데이터로 logistic regression을 해보겠다.
'Studying > Machine Learning' 카테고리의 다른 글
| [머신러닝] Overfitting & Regularization (with Polynomial function) (0) | 2022.07.12 |
|---|---|
| [머신러닝] Logistic Regression - 타이타닉 탑승자 사망여부 예측 (0) | 2022.07.11 |
| [머신러닝] Multiple Linear Regression - 연비(MPG) 예측 (0) | 2022.07.07 |
| [머신러닝] Linear Regression - 지구 온도 변화 분석 (0) | 2022.07.05 |
| [머신러닝] Linear regression(선형 회귀) 구현 (0) | 2022.07.05 |




댓글