2022.07.07 - [Studying/Machine Learning] - [머신러닝] Logistic Regression
[머신러닝] Logistic Regression
이전의 두 포스트에서는 데이터와 잘 맞는 직선을 찾는 linear regression을 했는데 예측 값이 떨어져 있다면 이 모델로는 예측이 어려울 것이다. 가장 대표적인 것이 binary classification인데 예측값이 0
gm-note.tistory.com
이전 포스팅에서 정리한 Logistic Regression을 실제 데이터에 적용해보려고 한다.
Data
우선 모듈을 import 해온다.
import sympy
import numpy
import numpy as np
import pandas as pd
from matplotlib import pyplot #시각화용
%matplotlib inline #colab환경에서 inline으로 볼 수 있도록
데이터는 scikit-learn(sklearn)의 데이터를 사용하겠다.
from sklearn.datasets import fetch_openml
titanic = fetch_openml('titanic_1', cache=False)
X = titanic.data.astype('float') # pd.DataFrame
y = titanic.target.astype('int64')
X와 y의 데이터가 어떻게 생겼는지 확인을 해보자
data_df = pd.concat((X,y), 1)
data_df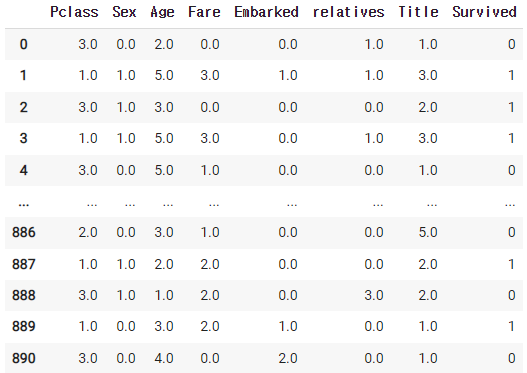
이렇게 X는 (891,7), y는 (891,)인 것을 확인했다.
Learning
이제 parameter를 계산해보겠다.
사용하는 함수는 이전 포스트에서도 사용했던 autograd를 사용하겠다.
# import the autograd-wrapped version of numpy
from autograd import numpy
# import the gradient calculator
from autograd import grad
x와 y를 numpy형태로 변환한다.
X_data = X.to_numpy()
y_data = y.to_numpy()
실제 데이터에 적용할 때는 데이터를 normalize 하는 것이 중요하다. 정규 분포로 일반화하겠다.
def z_score_norm(x):
mean = x_data.mean(0)
stdev = x_data.std(0)
return (x - mean)/stdev
x_data = z_score_norm(x_data)일반화가 완료되면 정규분포를 따르는 데이터로 변환된다.
X의 feature수가 7개이고 예측할 값은 하나이므로 w는 (7), b는 (1)의 shape를 가지게 된다.
numpy.random.seed(0)
w = numpy.random.randn(7)
b = numpy.random.randn(1)
params = [w, b]
데이터가 891개지만 복제를 따로 하지 않고 예전에 정리했던 numpy의 broadcasting을 이용하면 된다.
링크를 첨부해놓겠다. 2022.06.23 - [Studying/Machine Learning] - [머신러닝] 파이썬 Numpy - Numpy의 유용한 기능들
[머신러닝] 파이썬 Numpy - Numpy의 유용한 기능들
2022.06.21 - [Studying/Machine Learning] - [머신러닝] 파이썬 Numpy - Numpy indexing과 slicing [머신러닝] 파이썬 Numpy - Numpy indexing과 slicing 2022.06.20 - [Studying/Machine Learning] - [머신러닝]..
gm-note.tistory.com
학습을 위해 모델과 cost function을 정의한다.
def logistic(z):
return 1 / (1 + numpy.exp(-z))
def logistic_model(params, x):
w = params[0][None, :] #(7,) -> (1, 7)
b = params[1]
z = (w * x).sum(1) + b #w@x + b를 해도 되지만 이해를 위해 *연산을 사용
y = logistic(z)
return y
def log_loss(params, model, x, y):
y_pred = model(params, x)
return -numpy.mean(y * numpy.log(y_pred) + (1-y) * numpy.log(1 - y_pred))
gradient 함수를 정의하고 기울기 값을 계산해본다.
gradient = grad(log_loss)
gradient(params, logistic_model, x_data, y_data)
# [array([ 0.12413585, -0.11242071, 0.11475134, -0.0241943 , 0.1926073 ,
# 0.00565702, -0.03781919]), array([0.0650319])]이렇게 w와 b가 각각 나오게 된다.
저번 포스트와 같이 gradient descent를 진행해 보겠다.
max_iter = 5000
i = 0
# params가 w,b로 분리되어 있으므로 descent 분리
descent = [numpy.ones(len(params[0])),
numpy.ones(len(params[1]))]
while numpy.linalg.norm(np.concatenate((descent[0],descent[1]))) > 0.00001 and i < max_iter:
descent = gradient(params, logistic_model, x_data, y_data)
# params가 w,b로 분리되어 있으므로, 각각 업데이트
# learning rate = 0.1
params[0] = params[0] - descent[0] * 0.1
params[1] = params[1] - descent[1] * 0.1
i += 1
if i % 100 == 0:
print('n_iter {} descent norm - {:.6f}'.format(i, numpy.linalg.norm(np.concatenate((descent[0],descent[1])))))
이렇게 모델 학습이 끝난다.
Prediction
이제 실제 예측을 진행해보겠다.
0.5가 넘으면 1 아니면 0으로 분류하는 함수를 정의한다.
def decision_boundary(y):
return 1 if y >= .5 else 0
decision_boundary = numpy.vectorize(decision_boundary)
def classify(predictions):
return decision_boundary(predictions)vectorize를 사용하는 이유는 이전 포스트에서의 이유와 같이 시간이 오래 걸리기 때문이다.
그럼 예측값을 데이터에 추가해서 확인해 보겠다.
prediction = classify(logistic_model(params, x_data))
data_df['Prediction'] = prediction
data_df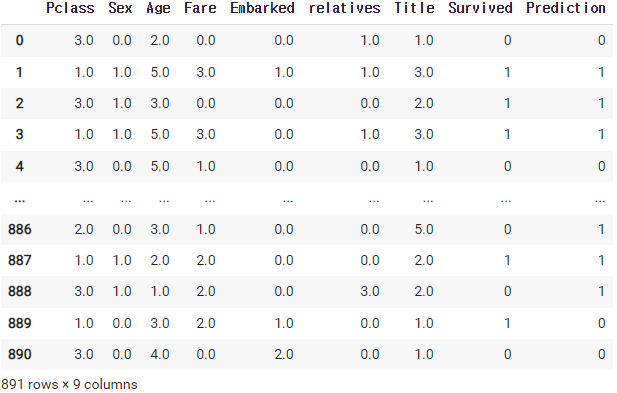
예측값의 정확도를 측정해보자.
data_df['IsCorrect'] = (data_df['Prediction'] == data_df['Survived']) # 실제 값과 예측 값이 동일하면 정답
Accuracy = data_df['IsCorrect'].mean()
print('정확도: {:.2f}%'.format(Accuracy*100))
# 정확도: 81.03%약 81 퍼센트 정도 예측을 하는 것을 확인할 수 있다.
확률을 높이기 위해서는 learning rate나 epoch(iteration)를 조절하면 될 것이다.
'Studying > Machine Learning' 카테고리의 다른 글
| [머신러닝] K-Means Clustering 정리 (0) | 2022.07.15 |
|---|---|
| [머신러닝] Overfitting & Regularization (with Polynomial function) (0) | 2022.07.12 |
| [머신러닝] Logistic Regression (0) | 2022.07.07 |
| [머신러닝] Multiple Linear Regression - 연비(MPG) 예측 (0) | 2022.07.07 |
| [머신러닝] Linear Regression - 지구 온도 변화 분석 (0) | 2022.07.05 |




댓글